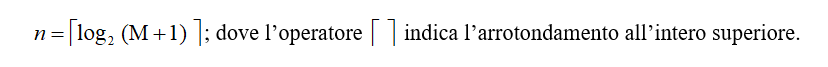Sistemi di numerazione: binario, ottale, esadecimale
Di seguito è riportata una descrizione dei sistemi di numerazione maggiormente utilizzati da un calcolatore elettronico, in particolare la rappresentazione dei numeri in binario puro, in modulo e segno, in complemento a uno, in complemento a due, in virgola fissa e mobile. Segue anche un accenno ai codici numeri e alfanumerici.
1.3.1 Conversione da base N a base
1.3.2 Conversione da base 10 a base N
1.3.3 Conversione da base 2 a base 8 o base 16
1.3.4 Conversione da base N a M
1.4 Intervallo di Rappresentazione IN BINARIO PURO
1.6 Rappresentazione dei numeri relativi
1.6.1 Rappresentazione in modulo e segno
1.6.2 Rappresentazione in complemento a 1 (c. a 1)
1.6.3 Rappresentazione in complemento a 2 (c. a 2)
1.1 Introduzione
Gli strumenti di calcolo hanno una origine antica che risale alla preistoria. L’uomo primitivo cominciò a indicare il totale degli animali abbattuti durante la caccia per mezzo di un insieme di tacche incise su un bastone o su un osso. In Repubblica Ceca è stato trovato, per esempio, un osso di lupo che presenta incisioni che forniscono una prova del fatto che l’idea di numero è molto antica.
Ad un certo punto della storia si presentò l’esigenza di un sistema che permettesse di indicare i numeri, a voce e per iscritto, impiegando poche parole e pochi segni fondamentali. Ogni popolo escogitò un proprio sistema di numerazione parlato e scritto; il sistema decimale si diffuse nel mondo come conseguenza del fatto che gli uomini iniziarono a contare con le dita.
Gli antichi sistemi di numerazione sono non posizionali. Per esempio nella rappresentazione romana i due numeri XII e XIX hanno la seconda cifra che pur avendo la stessa posizione assume nei due numeri due pesi diversi:
XII = 10 + 1 + 1
XIX = 10 + 10 – 1
Questo approccio rende difficile le operazioni aritmetiche, così nel tempo si affermarono i sistemi di numerazione posizionali. Con questo approccio, per eseguire i conteggi, si tracciavano delle righe per terra e fra una riga e l’altra si collocavano delle pietruzze che costituivano le unità contate. Gli spazi compresi tra le righe corrispondevano ai vari ordini e ciascuna pietruzza valeva una unità dell’ordine corrispondente allo spazio nel quale era collocata, sicché il suo valore dipendeva dalla sua posizione rispetto alle righe.
La numerazione posizionale con l’utilizzo delle cifre ci viene dall’India, dove le prime tracce di tale sistema risalgono al VI sec. d.C., ma la sua origine è ignota. Dopo l’anno 1000 fece la sua apparizione in Occidente per opera degli Arabi, la cui civiltà era più vicina a quella indiana. Nel 1202 l’italiano Leonardo Pisano, detto Fibonacci, dopo aver appreso durante i suoi viaggi in Oriente l’aritmetica coltivata dagli Arabi, la diffuse in Europa con il suo trattato Liber Abaci (libro dell’arte di fare i conti).
Più recentemente con lo sviluppo delle tecnologie elettroniche si sono costruiti i primi calcolatori elettronici. Per semplificare il più possibile i circuiti elettronici interni si è utilizzato il sistema di numerazione binario che fa uso delle sole cifre 0 e 1 per rappresentare i numeri. Per un circuito elettronico è facile distinguere un livello alto di tensione, associando la cifra 1, e un livello di tensione basso, associando la cifra 0. Pertanto nei prossimi paragrafi verrà analizzato nel dettaglio tale sistema di numerazione perché di fondamentale importanza in tutte le discipline che abbracciano l’elaborazione elettronica dell’informazione.
1.2 Sistemi di numerazione
Lo scopo di un sistema di numerazione è quello di rappresentare con delle cifre un numero. Il sistema che utilizziamo quotidianamente è il sistema decimale che fa uso di 10 cifre (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Fin dall’infanzia siamo stati abituati a contare facendo riferimento all’abaco dell’insegnante per determinare le unità, le decine, le centinaia, le migliaia e così via dei numeri.
In questa ottica noi sappiamo che il numero 436 è costituito da:
4 centinaia + 3 decine + 6 unità = 4 · 102 + 3 · 101 + 6 · 100 = 436
Il numero 10 è la base del sistema di numerazione e rappresenta il numero di cifre con cui rappresentiamo i numeri. Di fondamentale importanza è la posizione delle cifre perché cambia il peso associato.
Tutto questo è un concetto astratto; nulla ci vieta di cambiare la regola e di rappresentare i numeri utilizzando un numero diverso di cifre, cioè una base diversa. Per l’uomo è stato intuitivo utilizzare 10 cifre visto che si è iniziato a contare utilizzando le dita della mani, ma potrebbe essere più semplice, in altri contesti, utilizzare un numero di cifre diverso per semplificare le operazioni.
Qualunque intero N > 1 può essere scelto come base, ed ogni numero M può essere scritto nella forma:
M = an-1 · Nn-1 + an-2 · Nn-2 + … + a1 · N1 + a0, con 0≤ai≤N-1
Regole per determinare il valore nella base 10:
Regola 1
Partendo dalla cifra più significativa, si moltiplica la cifra per il valore della base elevata alla potenza corrispondente alla posizione.
Regola 2
Partendo dalla cifra più significativa, si moltiplica la cifra per il valore della base e si somma la cifra precedente alla più significativa, sul risultato si applica la stessa regola fino a sommare la cifra meno significativa come si intuisce analizzando la seguente formula:
M =[[[ an-1 · N + an-2] · N + an-3] · N + … + a1] · N + a0
1.2.1 Sistema Binario
Il computer è un sistema costituito da circuiti elettronici che riescono a distinguere con facilità due soli livelli logici: “0” e “1”, associati ad uno stato alto e basso di tensione. Pertanto si utilizza il sistema binario con base 2 e cifre 0,1.
Le cifre di un numero binario vengono chiamate “bit” (che è la contrazione di BInary digiT) il cui pesi dipendono dalla posizione e corrispondono a potenze di 2. Occorre tenere presente che un sicuro inconveniente di tale sistema è che occorrono più cifre binarie (o molti bit) per rappresentare i numeri rispetto al numero di cifre in decimali.
Con questa scelta un generico numero è rappresentato come:
M = bn-1 · 2n-1 + bn-2 · 2n-2 + … + b1 · 21 + b0, con 0≤bi≤1
Applicando la regola 1
1012= 1 · 22 + 0 · 21 + 1 · 20 = 4 + 0 + 1 = 5
Applicando la regola 2
[1 · 2 + 0] · 2 + 1 = 5
Analogamente al sistema decimale potremmo descrivere il numero come costituito da:
1 quaterna + 0 coppie + 1 unità = 5
In seguito si intende la base 10 per quei numeri che non hanno la base espressa come pedice.
La progressione dei numeri in un sistema binario avviene in modo analogo a quello decimale, dopo aver contato le cifre fondamentali in una posizione si ricomincia a contare introducendo un riporto sulla cifra a sinistra e così in cascata per tutte le posizioni. Vediamo un confronto con il sistema decimale:
| Decimale | Binario |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
Nel sistema decimale devo “contare dieci” per passare alla decina successiva con un riporto di uno, mentre nel sistema binario devo “contare due” per introdurre un riporto sulla cifra successiva.
1.2.2 Sistema Ottale
Oltre alla base 2 spesso per rappresentare i numeri, soprattutto per scrivere numeri binari più compatti, si usa la base 8, e le cifre a disposizione sono (0, 1, 2, 3, 4, 5, 6, 7).
Esempio:
5318 = 5 · 82 + 3 · 81 + 1 · 80 = 320 + 24 + 1 = 345
1.2.3 Sistema Esadecimale
Sempre con lo scopo di compattare l’informazione binaria al fine di manovrarla senza dover portare dietro un numero molto grande di bit si utilizza la base 16, che è un’altra potenza di due, non a caso, ma per rendere il passaggio tra le basi esaminate molto semplice. Le cifre a disposizione sono 16 quindi ne abbiamo 6 in più rispetto al sistema decimale, pertanto introduciamo le prime 6 lettere dell’alfabeto (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Esempio:
6Bh = 6 · 161 + 11 · 160 = 96 + 11 = 107
1.3 Conversione di base
Nel seguito vedremo le regole per il passaggio di un numero da una base ad un’altra utilizzando le basi che più ci interessano e cioè il passaggio da binario, ottale, esadecimale a decimale e viceversa.
1.3.1 Conversione da base N a base 10
Per il passaggio da una base N generica alla base 10 si possono seguire le due regole presentate nel paragrafo 1.1.
1.3.2 Conversione da base 10 a base N
Se consideriamo l’espressione introdotta nel paragrafo 1.1:
M = an-1 · Nn-1 + an-2 · Nn-2 + … + a1 · N1+ a0
che può essere riscritta come:
M = N · [ an-1 · Nn-2 + an-2 · Nn-3 + … + a1] + a0 = N · Q0 + ro
notiamo subito come la cifra a0 della rappresentazione del numero M nella base N, si ottiene come resto della divisione del numero M per la base N.
Le altre cifre della rappresentazione si ottengono iterando l’algoritmo al quoziente, per esempio la cifra a1:
Q0 = N · [an-2 · Nn-3 + an-3 · Nn-4 + … + a2] + a1 = N · Q1 + r1
Regola
Si effettuano divisioni successive per il valore della base e si prendono, alla rovescia, i singoli resti delle divisioni per rappresentare il numero.
Esempio: Conversione del numero 109 in base 2,8,16: 109 : 2 = 54 + 1 109 : 8 = 13 + 5 109 : 16 = 6 + D (13) 54 : 2 = 27 + 0 13 : 8 = 1 + 5 6 : 16 = 0 + 6 27 : 2 = 13 + 1 1 : 8 = 0 + 1 13 : 2 = 6 + 1 6 : 2 = 3 + 0 3 : 2 = 1 + 1 1 : 2 = 0 + 1 109 = 11011012 109 = 1558 109 = 6D16
Regola
Un metodo alternativo di conversione da base 10 a base 2 fa uso della tabella delle potenze di 2. Ad ogni passo si prende la più alta potenza di 2 inferiore al numero decimale; si assegna la cifra 1 alla posizione corrispondente all’esponente della massima potenza di 2. Si sottrae il numero di partenza e si ripete il procedimento finché il numero è diverso da 0.
Supponiamo di voler convertire in base 2 il numero decimale 2453:
211 = 2048 < 2453 allora bit posizione 11 = 1; 2453 – 2048 = 405 210 = 1024 > 405 allora bit posizione 10 = 0; 29 = 512 > 405 allora bit posizione 9 = 0; 28 = 256 < 405 allora bit posizione 8 = 1; 405 – 256 = 149 27 = 128 < 149 allora bit posizione 7 = 1; 149 – 128 = 21 26 = 64 > 21 allora bit posizione 6 = 0; 25 = 32 > 21 allora bit posizione 5 = 0; 24 = 16 < 21 allora bit posizione 4 = 1; 21 – 16 = 5 23 = 8 > 5 allora bit posizione 3 = 0; 22 = 4 < 5 allora bit posizione 2 = 1; 5 – 4 = 1 21 = 2 > 1 allora bit posizione 1 = 0; 20 = 1 = 1 allora bit posizione 0 = 1; 1 – 1 = 0 2453 = 1001100101012
1.3.3 Conversione da base 2 a base 8 o base 16
Un caso particolare di conversione da base N a base M si ha quando si deve passare da base 2 alla base 8 o 16 (o viceversa).
Il calcolo è semplificato perché:
- ogni cifra ottale (0, 1, 2, 3, 4, 5, 6, 7) è esprimibile nella corrispondente codifica binaria
(000, 001, 010, 011, 100, 101, 110, 111) su 3 cifre binarie.
- ogni cifra esadecimale (0, 1, 3, … , D, F) è esprimibile nella corrispondente codifica binaria (0000, 0001, 0010, 0011, … , 1110, 1111) su 4 cifre binarie.
Regola
Per passare dalla base 2 alla base 8 si raggruppano, a partire dal bit meno significativo, le cifre binarie in gruppi da 3 per esprimere una cifra ottale. Nell’ultimo gruppo si suppone che ci siano zeri se vi sono meno di 3 bit. Ovviamente, per passare dalla base 8 alla base 2 si esegue il ragionamento inverso.
Esempio:
10010101000101102=(001)2(001)2(010)2(100)2(010)2(110)2 = 1124268
24358 = (010)2(100)2(011)2(101)2 = 0101000111018
Regola
Per passare dalla base 2 alla base 16 si raggruppano, a partire dal bit meno significativo, le cifre binarie in gruppi da 4 per esprimere una cifra esadecimale. Nell’ultimo gruppo si suppone che ci siano zeri se vi sono meno di 4 bit. Ovviamente, per passare dalla base 16 alla base 2 si esegue il ragionamento inverso.
11010101000101102 = (1101)2(0101)2(0001)2(0110)2 = D51616 A3D16 = (1010)2(0011)2(1101)2 = 1010001111012
1.3.4 Conversione da base N a M
In generale conviene fare la conversione da base N a base 10 seguita dalla conversione da base 10 a M.
1.4 Intervallo di Rappresentazione IN BINARIO PURO
Abbiamo parlato di codifica di numeri in binario intendendo che avevamo a che fare con numeri interi positivi, o numeri naturali (ℕ). Ma a questo punto ci poniamo la domanda di sapere con n bit il massimo valore rappresentabile in binario. Per fare questo facciamo riferimento alla base 10 per poi estendere la regola alla base 2.
Con 3 cifre decimali possiamo rappresentare al massimo il numero 999 che altro non è:
103 – 1 = 1000 – 1 = 999, dove 10 è la base ed 3 è il numero di cifre.
Quindi in generale potremmo dire che con n cifre in una base N possiamo rappresentare i numeri M compresi tra:
0 ≤ M ≤ Nn – 1;
in particolare con N = 2:
0 ≤ M ≤ 2n – 1;
Per esempio con 4 bit riesco a rappresentare i numeri tra 0 e 15.
Viceversa volendo conoscere in numero n di bit necessari per rappresentare un numero M, si deve utilizzare la seconda espressione e passare ai logaritmi in base 2:
n ≥ log2 (M+1)
o meglio si prende la parte intera superiore visto che n deve essere un numero intero
Per esempio, volendo rappresentare il numero 9 occorrono:
1.5 Aritmetica in binario
Le operazioni aritmetiche in binario seguono le stesse regole delle operazioni in decimale.
1.5.1 Addizione
Per addizionare due numeri binari si seguono le seguenti regole:
- i due numeri sono incolonnati uno sopra l’altro
- si effettua la somma delle cifre di pari peso
- si può avere un riporto (carry) sul bit immediatamente superiore
Ai = bit in posizione i del numero binario A
Bi = bit in posizione i del numero binario B
Si = bit in posizione i del numero binario S = A + B
Ri = riporto sul bit i + 1
Ai + Bi = Si Ri 0 + 0 = 0 0 0 + 1 = 1 0 1 + 0 = 1 0 1 + 1 = 0 1
Esempio: A = 1 1 1 1 0; B = 1 0 1 0 0;
1 1 1 Riporto 1 1 1 1 0 + A 1 0 1 0 0 = B ----------- 1 1 0 0 1 0 Somma
1.5.2 Sottrazione
Per sottrarre due numeri binari si seguono le seguenti regole:
- i due numeri sono incolonnati uno sopra l’altro
- si effettua la sottrazione delle cifre di pari peso
- si può avere un prestito (borrow) sul bit immediatamente superiore
Ai = bit in posizione i del numero binario A
Bi = bit in posizione i del numero binario B
Si = bit in posizione i del numero binario S = A – B
Bi = prestito sul bit i + 1
Ai - Bi = Si Pi 0 - 0 = 0 0 0 - 1 = 1 1 1 - 0 = 1 0 1 - 1 = 0 0
Esempio: A = 1 0 1 1; B = 0 1 0 1;
1 Prestito 1 0 1 1 - A 0 1 0 1 = B ------- 0 1 1 0 Sottrazione
1.5.3 Overflow
Nel caso in cui si abbia un numero limitato di bit a disposizione (come avviene nella realtà), si possono avere due casi particolari di errore:
- carry sul bit più significativo (MSB – most significant bit).
- borrow dal bit più significativo (MSB – most significant bit).
In entrambi i casi il numero di bit fissato non è sufficiente per rappresentare il risultato.
Tale condizione si dice condizione di overflow (tracimazione).
Esempi:
Considerando i numeri binari di 4 bit, effettuare la somma 9 + 7.
9 = 10012 7 = 01112 1 1 1 1 1 0 0 1 + 0 1 1 1 = --------- 1 0 0 0 0
Il numero 16 non può essere rappresentato su 4 bit, quindi abbiamo overflow.
Considerando i numeri binari di 4 bit, effettuare la somma 5 – 7.
5 = 01012 7 = 01112 1 1 1 0 1 0 1 - 0 1 1 1 = --------- 1 1 1 0
Il numero che vogliamo rappresentare è un numero negativo e non abbiamo ancora visto la rappresentazione di numeri con segno quindi si ha un overflow.
1.5.4 Scalamento a sinistra
Uno scalamento (shift) a sinistra di un numero binario equivale ad una moltiplicazione per 2.
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
Scalando di una posizione a sinistra ho:
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Allo stesso modo il bit più significativo viene perso e se la rappresentazione ha un numero n fisso di bit, se la cifra scartata è 1 si ha overflow.
Se scalo di N posizioni ottengo una moltiplicazione per 2N.
1.5.5 Scalamento a destra
Uno scalamento (shift) a destra di un numero binario equivale a dividere per 2.
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
Scalando di una posizione a destra ho:
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
Allo stesso modo il bit meno significativo (least significant bit – LSB) viene perso e se la rappresentazione ha il bit meno significativo ad 1 abbiamo perdita di informazione (underflow). I numeri dispari non possono essere divisi per due o multipli quindi è inevitabile la perdita di informazione se non si introduce la parte frazionaria del numero.
Se scalo di N posizioni ottengo una divisione per 2N.
1.6 Rappresentazione dei numeri relativi
Abbiamo visto che nel caso della sottrazione si può avere un prestito sulla cifra più significativa a causa del fatto che si tenta di fare la sottrazione tra un numero A e B con A minore di B.
Quindi si deve trovare una rappresentazione per i numeri negativi, o meglio, una rappresentazione per i numeri interi relativi (ℤ). Esistono tre metodi principali per rappresentare numeri con segno:
- Rappresentazione modulo e segno.
- Rappresentazione in complemento a uno.
- Rappresentazione in complemento a due.
1.6.1 Rappresentazione in modulo e segno.
È un modo per rappresentare numeri interi relativi (ℤ) su un numero fisso di bit.
Se abbiamo n bit a disposizione, il bit più significativo indica il segno i restanti n-1 il valore assoluto del numero, in binario puro.
| S | Modulo |
S=0: numeri positivi (+)
S=1: numeri negativi (-)
Emerge subito un inconveniente di tale rappresentazione in quanto si hanno due rappresentazione per lo zero:
| 0 | 00000 …. 000000 |
| 1 | 00000 …. 000000 |
Per effettuare la conversione si scorpora il numero in due parti:
- il bit più significativo è decodificato come segno
- gli n-1 bit meno significativi sono decodificati come valore assoluto del numero relativo.
Utilizzando la codifica in modulo e segno, un numero M espresso su n bit potrà assumere i valori compresi tra:
– (2n-1-1) ≤ M ≤ 2n-1-1
Avere un bit dedicato al segno significa eseguire le operazioni di somma e sottrazione seguendo un algoritmo che tiene conto dei segni, tutto questo porta ad un procedimento laborioso che non conviene farlo eseguire ad un circuito elettronico; l’ideale sarebbe utilizzare una rappresentazione che permetta di eseguire le operazioni aritmetiche in modo che l’operazione di sottrazione si trasformata ricondotta ad una somma, in moda da utilizzare lo stesso stesso circuito, e dia un modo per capire se l’operazione è stata eseguita correttamente o meno (complemento a due).
1.6.2 Rappresentazione in complemento a 1 (c. a 1)
Un’altro modo per rappresentare i numeri relativi è la rappresentazione in c. a 1.
Per la conversione di un numero da decimale a c. a 1 si deve:
- Se il numero è positivo si prende la rappresentazione in binario puro a cui viene aggiunto il bit di segno con valore zero.
| 0 | modulo |
- Se il numero è negativo si complementano tutti i bit del modulo e si aggiunge il bit di segno con valore 1.
| 1 | modulo complementato |
Per complementazione si intende la procedura che inverte gli uno con gli zeri e viceversa. Anche in questo caso abbiamo una doppia rappresentazione dello zero che è un aspetto negativo.
Abbiamo, però, migliorato il problema delle operazioni aritmetiche infatti se vogliamo fare una somma tra numeri utilizziamo le stesse regole viste per il binario puro solo che il riporto sul bit più significativo viene sommato al bit meno significativo, analogamente per la sottrazione.
L’intervallo dei valori che si può rappresentare con n bit è:
– (2n-1-1) ≤ M ≤ 2n-1-1
Se consideriamo il caso di n=4 abbiamo un intervallo che va da -7 a +7.
+ 7 = 0111 + 6 = 0110 + 5 = 0101 + 4 = 0100 + 3 = 0011 + 2 = 0010 + 1 = 0001 + 0 = 0000 - 0 = 1111 - 1 = 1110 - 2 = 1101 - 3 = 1100 - 4 = 1011 - 5 = 1010 - 6 = 1001 - 7 = 1000
Esempi:
1 11 + 3 0011 + - 3 1100 + + 2 0010 = - 2 1101 = ------------- ------------ + 5 0101 1001 1 sommo il riporto - 5 1010 1 1 + 3 0011 + - 3 1100 - - 5 1010 = + 2 0010 = ------------ --------- - 2 1101 - 5 1010 1 11 - 6 1001 + + 3 0011 - - 1 1110 = - 1 1110 = ------------ --------- 0111 0101 1 sommo il riporto 1 sottraggo il prestito - 7 1000 + 4 0100
Problema dell’overflow si ha quando non si riesce a rappresentare il numero, ottenuto come somma di due operandi concordi, con il numero di bit a disposizione, per esempio con 4 bit riusciamo a rappresentare i numeri tra -7 e 7. La condizione di overflow si può verificare quando il risultato è di segno opposto agli operandi concordi. Con segni discordi non si ha mai overflow nella somma.
11 1 11 + 6 0110 + - 6 1001 + + 2 0010 = - 4 1011 = ---------- --------- 1000 <- overflow 0100 1 0101 <- overflow
Il c. a 1 presenta due rappresentazioni per lo zero, ma si preferisce usare quella di tutti 1 perché se sommo due numeri uguali in modulo ma di segno opposto ottengo il risultato 0 nella rappresentazione di tutti 1.
- 3 1100 + + 3 0011 = --------- - 0 1111
1.6.3 Rappresentazione in complemento a 2 (c. a 2)
Il problema di fondo delle rappresentazioni di numeri relativi è quello di ricondurre l’operazione di sottrazione ad una somma, così con lo stesso circuito eseguo due operazioni. Per fare questo consideriamo due numeri A e B positivi (A≥B) e l’operazione di sottrazione A-B, se si definisce il numero:
B’ = 2n – B
come il complemento alla base due del numero B, ottengo che la sottrazione A-B può essere vista come:
A + B’= A – B + 2n, a patto di non considerare il termine 2n che rappresenta il riporto sulla cifra n+1 (cifra più significativa).
Potremmo fare un esempio con i numeri decimali per comprendere meglio questo concetto.
Supponiamo di avere due sole cifre (n=2) e che vogliamo eseguire la sottrazione tra il numero A=69 e B=56:
B’ = 102 – 56 = 44
1 <- ignoro il riporto
69 +
44 =
----
13
A questo punto dopo aver visto il perché del complemento a 2 vediamo come convertire un numero da decimale in c. a 2.
- Se il numero è positivo si prende la rappresentazione in binario puro a cui viene aggiunto il bit di segno con valore zero.
| 0 | modulo |
- Se il numero è negativo:
- Si scrive i corrispondente numero positivo in c. a 2.
- Si complementano tutti i bit (c. a 1)
- Si somma 1
Osservazione: i numeri negativi hanno sempre il bit di segno negativo esiste una sola rappresentazione dello zero, ed è costituita da tutti zeri.
Un modo alternativo di ottenere la rappresentazione in c. a 2 di un numero negativo è la seguente:
- Si scrive il numero come se fosse positivo
- Copio tutti gli zeri fino a trovare il primo uno
- Copio l’uno trovato
- Complemento i restanti bit
Avendo un solo zero la scala dei valori rappresentati non è simmetrica, infatti con n bit abbiamo:
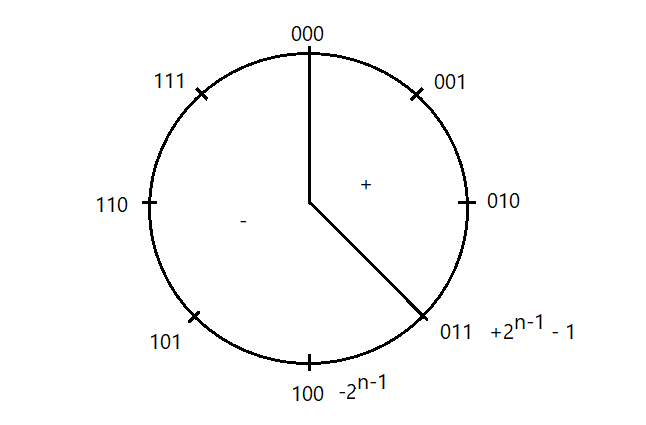
– 2n-1 ≤ M ≤ 2n-1-1
Con n = 4 da -8 a + 7.
+7 = 0111 +6 = 0110 +5 = 0101 +4 = 0100 +3 = 0011 +2 = 0010 +1 = 0001 +0 = 0000 -1 = 1111 -2 = 1110 -3 = 1101 -4 = 1100 -5 = 1011 -6 = 1010 -7 = 1001 -8 = 1000
Esempi:
111 1 +6 0110 + +6 0110 - -2 1110 = -2 1110 = +4 0100 -8 1000
Si ignora il riporto o il prestito sul bit più significativo a patto che il numero sia rappresentabile con i bit a disposizione.
Anche per il complemento a 2 si ha il problema dell’overflow quando si cerca di sommare due numeri di segno concorde il cui risultato non può essere rappresentato sul numero di bit previsti dalla rappresentazione. In questo caso il risultato è di segno opposto agli operandi di segno concorde.
1 1 +6 0110 + 7 0111 - +5 0101 = -2 1110 = 1011 <- overflow 1001 <- overflow
Se immaginiamo la scala dei valori precedenti con i numeri disposti su un cerchio, affiancando il valore positivo più alto con il valore negativo più basso, ci accorgiamo subito che sommare i numeri senza tenere conto del loro riporto significa girare sempre nel cerchio o percorrere la scala precedente dal basso verso l’alto per poi iniziare dal fondo. In questa ottica ho overflow ogni qualvolta l’operazione mi porta ad attraversare il salto di segno. Infatti sommando 6 a 5 ci porta fuori dai valori positivi, 11 non è rappresentabile con 4 bit in c. a 2, e ricominciamo a percorrere quelli negativi fermandoci sul -5.
1.7 Numeri frazionari
Nell’operazione di scalamento a destra abbiamo visto che se il bit meno significativo è uguale ad 1 abbiamo perdita di informazione poiché non possiamo dividere per 2 un numero dispari. Quindi per introdurre la parte frazionaria in un numero binario occorre aggiungere un numero di bit per rappresentazione della parte frazionaria tale da garantire la precisione richiesta.
1.7.1 Virgola fissa
Nella rappresentazione in virgola fissa si aggiungono m bit per la parte frazionaria con regole analoghe a quelle viste fino ad ora.
La rappresentazione è:
M = bn-1 2n-1 + bn-2 2n-2 + + b1 21+ b0 , c-1 2-1+ c-2 2-2 + c-m 2-m
Per convertire un numero da decimale a binario con parte frazionaria si deve:
- Si convertono separatamente la parte intera e la parte frazionaria
- Per la parte intera si segue la procedura già vista
- Per la parte frazionaria si effettuano moltiplicazioni successive per 2 separando la parte intera (0 o 1) da quella frazionaria così ottenuta:
-
- Il risultato della moltiplicazione è uno
- oppure si raggiunge la precisione richiesta
Esempio:
6,25
6 = 1102
0,25 · 2 = 0,5 + 0
0,50 · 2 = 0 + 1
110,012
0,625
0 = 02
0,625 · 2 = 0,25 + 1
0,25 · 2 = 0,50 + 0
0,50 · 2 = 0 + 1
0,1012
Si noti che in generale ad un numero frazionario decimale con un numero limitato di cifre può corrispondere un numero frazionario binario con un numero infinito di cifre. In tal caso ci si ferma alla precisione desiderata.
Esempio: Convertire 0,3 con precisione di 1/100
0,3 · 2 = 0,6 + 0
0,6 · 2 = 0,2 + 1
0,2 · 2 = 0,4 + 0
0,4 · 2 = 0,8 + 0
0,8 · 2 = 0,6 + 1
0,6 · 2 = 0,2 + 1
0,2 · 2 = 0,4 + 0
0,3 = (0,0100110….)2
L’errore è minore di 1/100 perché 1/27 =1/128.
La rappresentazione dei numeri in virgola fissa contiene intrinsecamente una limitazione pratica, poichè si mantiene un errore assoluto costante sull’intero intervallo di numeri rappresentato, quindi numeri grandi e numeri piccoli hanno la stessa precisione. Nelle applicazioni importa avere un errore relativo costante e cioè se il numero è grande ci interessa meno la parte frazionaria a differenza di numeri piccoli dove la parte frazionaria diventa consistente, per esempio:
1000,0001 ha una precisione di 10-4
1,0001 ha una precisione di 10-4
l’errore relativo nel primo caso è di 10-4/1000= 10-8
l’errore relativo nel secondo caso è di 10-4/1= 10-4
1.7.2 Virgola mobile
Nei calcoli scientifici si utilizzano numeri reali (ℝ) ed importante considerare un numero di cifre decimali che siano significative per l’operazione eseguita. Se il numero è piccolo è importante mantenere il maggior numero di cifre, se il numero è grande le cifre decimali diventano meno significative. A tele scopo quindi si utilizza la notazione scientifica per rappresentare i numeri reali affinché l’errore relativo resti all’incirca costante sull’intero intervallo dei numeri rappresentati.
Nel caso di numeri binari la rappresentazione in virgola mobile è una rappresentazione dei numeri che utilizza la notazione scientifica con potenze di 2:
M= mantissa · 2esponete
Il formato più utilizzato è quello IEEE P754 (precisione singola), rappresentato su 32 bit, nel modo seguente:
| S | Esponente (8 bit) | Mantissa (modulo 23 bit) |
L’esponente è rappresentato come numero senza segno su 8 bit in eccesso 127, cioè i valori da -126 a + 127 sono messi in corrispondenza con i valori da 0 a 255, per non dovere gestire anche il segno dell’esponente.
La mantissa è codificata in modulo e segno su 24 bit:
- La mantissa è sempre normalizzata nella forma 1.XXXXXX (l’uno viene omesso)
- Si rappresenta la parte frazionaria nei primi 23 bit meno significativi
- Il segno è dato dal bit più significativo dei 32 bit
La rappresentazione di un numero è quindi:
M= ± 1,XXXXX 2YYYYYY2
Esempio:
13,25 = 1101,012 = 1,10101 23
Exp= 3 + 127 = 100000102
Quindi la rappresentazione è:
0 10000010 10101000000000000000000
1.8 CODICI
In un canale di comunicazione la “sorgente” genera il segnale (quale che sia la sua natura) da trasmettere al ricevitore (cioè all’utente); tale segnale non viene però trasmesso così com’è, ma viene in qualche modo codificato da un opportuno dispositivo, che prende appunto il nome di “codificatore di canale”; il segnale codificato emesso dal codificatore viene inviato al canale di trasmissione, il quale rappresenta tutti quei dispositivi necessari per la trasmissione del segnale stesso.
1.8.1 Codici BCD pesati
Nei codici BCD (Binary Coded Decimal) un numero è diviso nelle cifre decimali che lo compongono, ed ogni cifra è codificata separatamente dalle altre su 4 bit. Tra questi il più conosciuto è il codice 8-4-2-1 (dal peso delle sue cifre).
0 0000 5 0101
1 0001 6 0110
2 0010 7 0111
3 0011 8 1000
4 0100 9 1001
Esempio:
471 = 0100 0111 0001
Molto importante è il codice 2-4-2-1 che ha la proprietà di essere autocomplementante.
0 0000 5 1011
1 0001 6 1100
2 0010 7 1101
3 0011 8 1110
4 0100 9 1111
Esempio:
406 = 0100 0000 1100
593 = 1011 1111 0011 = c.a 9
1.8.2 Codici BCD non pesati
Nei codici BCD (Binary Coded Decimal) non pesati vengono utilizzati nel caso di trasmissioni rumorose poichè sono robusti.
Tra questi abbiamo il codice eccesso 3 che si ottiene sommando 3 al codice 8-4-2-1; ogni cifra contiene almeno un 1 ed è autocomplementante.
0 0011 5 1000
1 0100 6 1001
2 0101 7 1010
3 0110 8 1011
4 0111 9 1100
Il codice 2 su 5 utilizza 5 bit e adotta solo le rappresentazioni che contengono due 1; ha buone proprietà di rilevamento degli errori ed è utilizzato per le letture automatiche dei numeri (codici a barre):
0 01100 5 00110
1 11000 6 10001
2 10100 7 01001
3 10010 8 00101
4 01010 9 00011
1.8.3 Codici Gray
Il codice Gray è un codice ciclico utilizzato per la codifica binaria di informazioni di tipo analogico (utilizzato dove richiesta una conversione analogico-digitale). Ha la proprietà di richiedere il cambiamento di un solo bit per passare da una configurazione alla successiva (nelle sintesi delle macchine sequenziali elimina la possibilità di corse critiche o stati di indeterminazione).
Per costruire il codice Gray si utilizza la seguente regola:
- Si aggiunge uno 0 a sinistra del numero binario
- Partendo da sinistra si sostituisce ad ogni coppia di bit adiacenti il nuovo bit secondo la tabella della funzione ex-or:
00 -> 0 10 -> 1
01 -> 1 11 -> 0
Dec. Binario Gray
0 000 000
1 001 001
2 010 011
3 011 010
4 100 110
5 101 111
6 110 101
7 111 100
1.8.4 Codici ASCII
La tabella ASCII è un codice convenzionale usato per la rappresentazione dei caratteri di testo attraverso i byte: ad ogni byte viene fatto corrispondere un diverso carattere della tastiera (lettere, numeri, segni).In realtà lo standard ASCII copre solo i primi 128 byte (da 00000000 a 01111111), i successivi byte fino al 256 costituiscono la tabella ASCII estesa che presenta varie versioni a carattere nazionale.
Nella tabella ASCII standard si trovano le cifre numeriche, le lettere maiuscole e minuscole (maiuscole e minuscole hanno codici ASCII differenti) la punteggiatura, i simboli aritmetici e altri simboli ($, &, %, @, #, ecc.). Essendo stata concepita in America, la tabella ASCII standard non comprende le lettere accentate (sconosciute all’ortografia inglese).
I primi 32 byte della tabella standard sono inoltre riservati per segnali di controllo e funzioni varie.